inducteurs dans les circuits à courant alternatif

 

À partir de l'équation vind = L(di/dt), la formule de la tension induite, vous pouvez voir que plus le courant à travers une inductance change rapidement, plus la tension induite sera élevée. Par exemple, si le taux de variation du courant est nul, la tension est nulle [vind = L(di/dt) = L(0) = 0 V]. Lorsque di/dt est un maximum positif, vind est un maximum positif ; lorsque di/dt est un maximum négatif, vind est un maximum négatif.

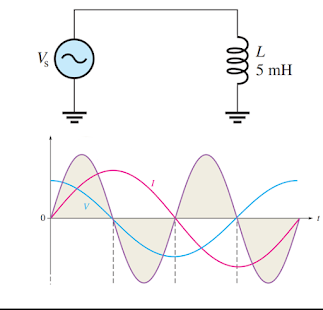
Lorsqu'un courant sinusoïdal est dans une inductance, le courant peut être exprimé mathématiquement comme i(t) = ip(sin 2πft). La courbe de courant a la même forme que la courbe sinusoïdale mathématique comme le montre la figure.

Le taux de variation de la fonction sinus est la fonction cosinus, qui devance la fonction sinus de 90°. Étant donné que la tension induite aux bornes de l'inductance est le taux de variation du courant, la tension est en avance de 90 ° sur le courant dans une inductance idéale, comme illustré à la figure .

Réactance inductive, XL

La réactance inductive est l'opposition au courant sinusoïdal, exprimée en ohms. Le symbole de la réactance inductive est XL.

Pour développer une formule pour XL, nous utilisons la relation vind = L(di/dt) et les courbes:

Le taux de variation du courant est directement lié à la fréquence.

Plus le courant change rapidement, plus la fréquence est élevée. Par exemple, vous pouvez voir cette courbe, la pente de l'onde sinusoïdale A aux passages par zéro est plus raide que celle de l'onde sinusoïdale B. Rappelez-vous que la pente d'une courbe en un point indique le taux de changement en ce point. L'onde sinusoïdale A a une fréquence plus élevée que l'onde sinusoïdale B, comme indiqué par un taux de changement maximal plus élevé (di/dt est supérieur aux passages par zéro)

Lorsque la fréquence augmente, di/dt augmente, et donc vind augmente. Lorsque la fréquence diminue, di/dt diminue, et donc vind diminue. La tension induite dépend directement de la fréquence.

Une augmentation de la tension induite signifie plus d'opposition (XL est plus grand). Par conséquent, XL est directement proportionnel à la tension induite et donc directement proportionnel à la fréquence.

À présent,

  si di/dt est constant et que l'on fait varier l'inductance, une augmentation de L produit une augmentation de vind, et une diminution de L produit une diminution de vind.

Encore une fois, une augmentation de vind signifie plus d'opposition (plus grand XL). Par conséquent, XL est directement proportionnel à la tension induite et donc directement proportionnel à l'inductance. La réactance inductive est directement proportionnelle à f et L.

La formule de la réactance inductive, XL, est:

La réactance inductive, XL, est en ohms lorsque f est en hertz et L est en henry. Comme pour la réactance capacitive, le terme 2π est un facteur constant dans l'équation, qui provient de la relation entre une onde sinusoïdale et le mouvement de rotation.

EXEMPLE:

Une tension sinusoïdale est appliquée au circuit.

La fréquence est de 10 kHz. Déterminer la réactance inductive.

SOLUTION:

Réactance pour les inducteurs en série

l'inductance totale des inducteurs série est la somme des

inductances individuelles. Comme la réactance est directement proportionnelle à l'inductance, la réactance totale des inducteurs en série est la somme des réactances individuelles.

Réactance pour les inductances parallèles

Dans un circuit alternatif avec des inductances parallèles, l'inductance totale est l'inverse de la somme des inverses des inductances. De même, la réactance inductive totale est l'inverse de la somme des inverses des réactances individuelles.

EXEMPLE:

Quelle est la réactance inductive totale de chaque circuit:

SOLUTION:

Les réactances des inducteurs individuels sont les mêmes dans les deux circuits:

Pour les inductances série du circuit (a), la réactance totale est la somme de XL1 et XL2,

Pour les inductances en parallèle dans le circuit (b),