Les nombres complexes permettent des opérations mathématiques avec des quantités de nombre complexe et sont utiles dans l'analyse des circuits à courant alternatif. Avec le système de nombres complexes, vous pouvez ajouter, soustraire, multiplier et diviser des quantités qui ont à la fois une amplitude et un angle, telles que des ondes sinusoïdales et d'autres quantités de circuit alternatif. La plupart des calculatrices scientifiques peuvent effectuer des opérations avec des nombres complexes. Consultez votre manuel d'utilisation pour connaître la procédure exacte.
Nombres positifs et négatifs
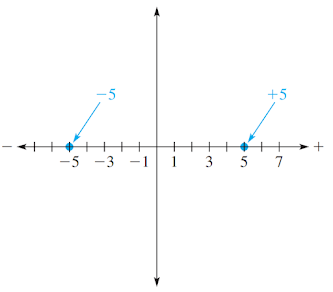
Les nombres positifs sont représentés par des points à droite de l'origine sur l'axe horizontal d'un graphique, et les nombres négatifs sont représentés par des points à gauche de l'origine,
De plus, les nombres positifs sont représentés par des points sur l'axe vertical au-dessus de l'origine, et les nombres négatifs sont représentés par des points en dessous de l'origine,
Le plan complexe
Pour distinguer les valeurs sur l'axe horizontal des valeurs sur l'axe vertical, un plan complexe est utilisé. Dans le plan complexe, l'axe horizontal est appelé l'axe réel et l'axe vertical est appelé l'axe imaginaire,
Note: Dans les travaux sur les circuits électriques, un préfixe ± j est utilisé pour désigner les nombres situés sur l'axe imaginaire afin de les distinguer des nombres situés sur l'axe réel. Ce préfixe est connu sous le nom d'opérateur j. En mathématiques, un i est utilisé à la place d'un j, mais dans les circuits électriques, le i peut être confondu avec le courant instantané, donc j est utilisé.Position angulaire sur le plan complexe
les positions angulaires sont représentées sur le plan complexe:
L'axe réel positif représente zéro degré. En procédant dans le sens
antihoraire, l'axe +j représente 90°, l'axe réel négatif
représente 180°, l'axe -j est le point 270° et, après
une rotation complète de 360°, vous êtes de retour à l'axe réel positif.
Notez que le plan est divisé en quatre quadrants.
Représentation d'un point sur le plan complexe
Un point sur l'axe +j à 6 unités de l'origine, est le nombre imaginaire
positif, +j6.
un point à 5 unités le long de l'axe - j est le nombre imaginaire négatif, -
j5 :
Lorsqu'un point ne se trouve sur aucun axe mais quelque part dans l'un des
quatre quadrants, il s'agit d'un nombre complexe et est défini par ses
coordonnées. Par exemple:
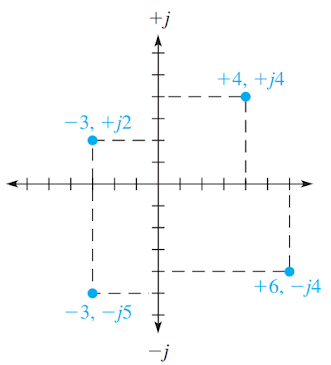
le point situé dans le premier quadrant a une valeur réelle de +4 et une
valeur j de +j4 et s'exprime par +4, +j4. Le point situé dans le deuxième
quadrant a pour coordonnées -3 et +j2. Le point situé dans le troisième
quadrant a pour coordonnées -3 et -j5. Le point situé dans le quatrième
quadrant a pour coordonnées +6 et - j4.
Valeur de j
Si vous multipliez la valeur réelle positive de +2 par j, le résultat est
+j2. Cette multiplication a effectivement déplacé le +2 d'un angle de 90°
vers l'axe +j. De même, multiplier +2 par -j le fait pivoter de -90° sur
l'axe -j. Ainsi, j est considéré comme un opérateur de rotation.
Mathématiquement, l'opérateur j vaut √(−1) . Si +j2 est multiplié par j,
vous obtenez:
Ce calcul place effectivement la valeur sur l'axe réel négatif. Par
conséquent, multiplier un nombre réel positif par j2
le convertit en un
nombre réel négatif, ce qui correspond en fait à une rotation de 180° sur le
plan complexe.
Formes rectangulaires et polaires
Rectangulaire et polaire sont deux formes de nombres complexes utilisés pour représenter les quantités de nombre complexe. Chacun présente certains avantages lorsqu'il est utilisé dans l'analyse de circuit, en fonction de l'application particulière. Une quantité de nombre complexe contient à la fois l'amplitude et la position angulaire ou la phase. Dans ce texte, les lettres italiques telles que V et I sont utilisées pour représenter uniquement la magnitude, et les lettres non italiques en gras telles que V et I sont utilisées pour représenter des quantités de nombre complexe complètes.
Forme rectangulaire
Une grandeur de nombre complexe est représentée sous forme rectangulaire par la somme algébrique de la valeur réelle (A) de la coordonnée et de la valeur j (B) de la coordonnée, exprimée sous la forme générale suivante :Des exemples de grandeurs de nombre complexe sont 1 + j2, 5 - j3, -4 + j4 et -2 - j6, Comme vous pouvez le voir, les coordonnées rectangulaires décrivent le nombre complexe en termes de ses valeurs projetées sur l'axe réel et l'axe j. Une "flèche" tracée de l'origine au point de coordonnées dans le plan complexe représente graphiquement la quantité de nombre complexe.
Forme polaire
Les quantités de nombre complexe peuvent également être exprimées sous forme polaire, qui se compose de la magnitude du nombre complexe (C) et de la position angulaire par rapport à l'axe réel positif (𝜃), exprimée sous la forme générale suivante :
Les exemples sont 2∠45 °, 5120 °, 4∠-110 ° et 8∠-30 °. Le premier nombre est la magnitude et le symbole précède la valeur de l'angle.
La longueur du nombre complexe, bien sûr, représente la magnitude de la quantité. N'oubliez pas que pour chaque nombre complexe exprimé sous forme polaire, il existe également une expression équivalente sous forme rectangulaire.
Conversion de la forme rectangulaire à la forme polaire
Un nombre complexe peut exister dans n'importe lequel des quatre quadrants du plan complexe, L'angle de phase 𝜃 dans chaque cas est mesuré par rapport à l'axe réel positif (0°), et 𝛷 (phi) est l'angle dans les 2ème et 3ème quadrants par rapport à l'axe réel négatif, comme indiqué ci-dessous :
La première étape pour passer de la forme rectangulaire à la forme polaire consiste à déterminer l'amplitude du nombre complexe. Un nombre complexe peut être visualisé comme formant un triangle rectangle dans le plan complexe,
pour chaque emplacement de quadrant. Le côté horizontal du triangle est la valeur réelle, A, et le côté vertical est la valeur j, B. L'hypoténuse du triangle est la longueur du nombre complexe, C, représentant la magnitude, et peut être exprimée à l'aide de la formule de Pythagore. théorème, comme:
Dans chaque cas, les signes appropriés doivent être utilisés dans le calcul. La formule générale pour convertir de rectangulaire en polaire est:
EXEMPLE:
Convertissez les nombres complexes suivants de la forme rectangulaire à la forme polaire en déterminant la magnitude et l'angle :
(a) 8 + j6
(b) 10 - j5
SOLUTION:
(b) L'amplitude de nombre complexe et l'angle représenté par 10 -j5 est:
𝜃 est l'angle par rapport à l'axe réel positif. La forme polaire de 108 - j5 est:
Conversion de la forme polaire à la forme rectangulaire
La forme polaire donne la grandeur et l'angle d'une quantité de nombre complexe,Pour obtenir la forme rectangulaire, vous devez trouver les côtés A et B du triangle, en utilisant les règles de la trigonométrie énoncées ci-dessous :
v




















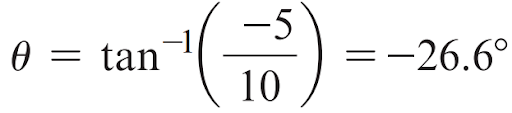




Post a Comment