L'énergie est stockée dans le champ électromagnétique d'un inducteur lorsqu'il est connecté à une source de tension continue. L'accumulation de courant à travers l'inducteur se produit de manière prévisible, qui dépend de la constante de temps du circuit. La constante de temps est déterminée par l'inductance et la résistance dans un circuit.
Lorsqu'il y a un courant continu constant dans une inductance, il n'y a pas de tension induite. Il y a cependant une chute de tension due à la résistance d'enroulement de la bobine. L'inductance elle-même apparaît comme un court-circuit à courant continu. L'énergie est stockée dans le champ électromagnétique selon la formule indiquée dans l'équation W= 1/2*LI2
Pour l'inductance, la seule conversion d'énergie en chaleur se produit dans la résistance de l'enroulement (P = I2RW ).
La constante de temps RL
Parce que l'action de base de l'inductance est de développer une tension qui s'oppose à une variation de son courant, il s'ensuit que le courant ne peut pas changer instantanément dans une inductance. Il faut un certain temps au courant pour passer d'une valeur à une autre. La vitesse à laquelle le courant change est déterminée par la constante de temps RL.La constante de temps RL est un intervalle de temps fixe égal au rapport de l'inductance à la résistance. La formule est:
où τ est en secondes lorsque l'inductance (L) est en henry et la résistance (R) est en ohms. Il est facile de montrer que l'unité d'inductance (henry), divisée par l'unité de résistance (ohm) est la seconde. le henry peut être écrit en (volt-seconde)/ampère. L'ohm (de la loi d'Ohm) est un volt/ampère.
EXEMPLE:Un circuit série RL a une résistance de 1,0 kΩ et une inductance de 2,5 mH. Quelle est la constante de temps ?
SOLUTION:
Courant dans une inductance
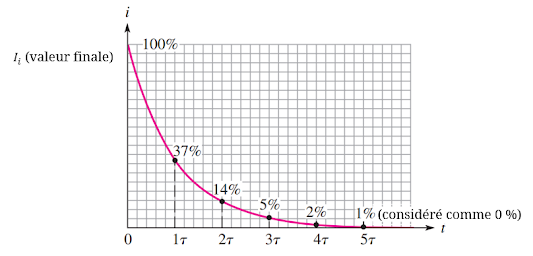
Augmentation du Courant Dans un circuit RL en série, le courant augmentera jusqu'à environ 63 % de sa valeur totale dans un intervalle de temps constant après l'application de la tension. Cette accumulation de courant est analogue à l'accumulation de tension de condensateur pendant la charge dans un circuit RC ; ils suivent tous deux une courbe exponentielle et atteignent les pourcentages approximatifs du courant final comme illustré .
Diminution du courant Le courant dans une inductance diminue de façon exponentielle selon les valeurs approximatives en pourcentage.
La variation du courant sur cinq intervalles de temps constant est illustrée dans le graphique. En pratique, lorsque le courant atteint sa valeur finale d'environ 0 A, il cesse d'évoluer. Avant l'ouverture de l'interrupteur, le courant traversant L est à une valeur constante de 10 mA, qui est déterminée par R1 car L agit idéalement comme un court-circuit. Lorsque l'interrupteur est ouvert, la tension d'inductance induite fournit initialement 10 mA via R2. Le courant diminue alors de 63% pendant chaque intervalle de constante de temps.
Réponse à une onde carrée
Un bon moyen de démontrer à la fois l'augmentation et la diminution du courant dans un circuit RL consiste à utiliser une tension d'onde carrée comme entrée. L'onde carrée est un signal utile pour observer la réponse en courant continu d'un circuit car elle fournit automatiquement une action d'activation et de désactivation similaire à un interrupteur.
Lorsque l'onde carrée passe de son niveau bas à son niveau haut, le courant dans le circuit répond en augmentant de manière exponentielle jusqu'à sa valeur finale. Lorsque l'onde carrée revient au niveau zéro, le courant dans le circuit répond en diminuant de manière exponentielle jusqu'à sa valeur zéro.
Les formules exponentielles
Les formules pour le courant exponentiel et la tension dans un circuit RL sont similaires pour le circuit RC, et les courbes exponentielles universelles s'appliquent aux inducteurs ainsi qu'aux condensateurs. Les formules générales pour les circuits RL sont énoncées comme suit :
où VF et IF sont les valeurs finales de la tension et du courant, Vi et Ii sont les valeurs initiales de la tension et du courant. Les lettres italiques minuscules v et i sont les valeurs instantanées de la tension et du courant de l'inductance à l'instant t.
Augmentation du courant : La formule pour le cas particulier dans lequel une courbe de courant exponentielle croissante commence à zéro est dérivée en définissant Ii = 0
EXEMPLE:
déterminer le courant de l'inductance 30 µs après la fermeture de l'interrupteur ?
SOLUTION:
La constante de temps RL est:
Le courant final est:
Le courant initial est nul. Notez que 30 µs est inférieur à une constante de temps, de sorte que le courant atteindra moins de 63 % de sa valeur finale pendant ce temps.
Diminution du courant: La formule pour le cas particulier dans lequel un courant exponentiel décroissant a une valeur finale de zéro est dérivée en définissant IF = 0
EXEMPLE:
quel est le courant à chaque intervalle de microseconde pour un cycle complet de l'onde carrée d'entrée, VS après avoir calculé le courant à chaque instant, esquissez la forme d'onde actuelle.
SOLUTION:
Lorsque l'impulsion passe de 0 V à 10 V à t = 0, le courant final est:
pour le courant croissant,
b

















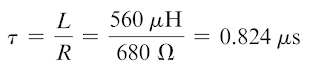




Post a Comment