condensateurs en CA
Comme vous le savez, un condensateur bloque le courant continu. Un condensateur laisse passer le courant alternatif mais avec une quantité d'opposition, appelée réactance capacitive, qui dépend de la fréquence du courant alternatif.
Pour expliquer pleinement le fonctionnement des condensateurs dans les circuits alternatifs, le concept de dérivée doit être introduit. La dérivée d'une quantité variant dans le temps est le taux de changement instantané de cette quantité.
Rappelons que le courant est le débit de charge (électrons). Par conséquent, le courant instantané, i, peut être exprimé comme le taux instantané de changement de charge, q, par rapport au temps, t.
Le terme dq/dt est la dérivée de q par rapport au temps et représente le taux de variation instantané de q. Aussi, en termes de quantités instantanées, q = Cv. Par conséquent, à partir d'une règle de base du calcul différentiel, la dérivée de q par rapport au temps est dq/dt = C(dv/dt). Puisque i = dq/dt, on obtient la relation suivante :
Cette formule indique:
Le courant instantané du condensateur est égal à la capacité multipliée par le taux de variation instantané de la tension aux bornes du condensateur.
Plus la tension aux bornes d'un condensateur change rapidement, plus le courant est important.
Relation de phase du courant et de la tension dans un condensateur
Considérez ce qui se passe lorsqu'une tension sinusoïdale est appliquée à travers un condensateur, comme le montre la figure:
La forme d'onde de tension a un taux de variation maximum (dv/dt = max) aux passages par zéro et un taux de variation nul (dv/dt = 0) aux pics, comme indiqué sur la figure:
La relation de phase entre le courant et la tension se produit lorsque le condensateur peut être établi à partir de l'équation i = C(dv/dt) . Lorsque dv/dt = 0, i est également égal à zéro car i = C(dv/dt) = C(0) = 0. Lorsque dv/dt est un maximum positif, i est un maximum positif ; lorsque dv/dt est un maximum négatif, i est un maximum négatif.
Lorsqu'une tension sinusoïdale est appliquée à un condensateur, la tension aux bornes du condensateur peut être exprimée mathématiquement par v(t) = Vp (sin 2πft). La courbe de tension a la même forme que la courbe sinusoïdale mathématique illustrée à la Figure :
Le taux de variation de la fonction sinus est la fonction cosinus, qui mène la fonction sinus de 90°. Étant donné que le courant est le taux de variation de la tension, le courant dans un condensateur idéal mène la tension de 90 °, comme illustré à la figure :
Réactance capacitive, XC
La réactance capacitive est l'opposition au courant sinusoïdal, exprimée en ohms. Le symbole de la réactance capacitive est XC .
Pour développer une formule pour XC, nous utilisons la relation i = C(dv/dt) et les courbes:
Le taux de changement de tension est directement lié à la fréquence. Plus la tension change rapidement, plus la fréquence est élevée.
Par exemple, vous pouvez voir que dans la Figure ci-dessus la pente de l'onde sinusoïdale A aux passages par zéro est plus raide que celle de l'onde sinusoïdale B. La pente d'une courbe en un point indique le taux de changement en ce point.
L'onde sinusoïdale A a une fréquence plus élevée que l'onde sinusoïdale B, comme indiqué par un taux de changement maximum plus élevé (dv/dt est plus grand aux passages à zéro).
Lorsque la fréquence augmente, dv/dt augmente, et donc i augmente. Lorsque la fréquence diminue, dv/dt diminue, et donc i diminue.
Une augmentation de i signifie qu'il y a moins d'opposition au courant ( XC est moins), et une diminution de i signifie une plus grande opposition au courant ( XC est plus grand). Par conséquent, XC est inversement proportionnel à i et donc inversement proportionnel à la fréquence.
XC est inversement proportionnel à f, représenté par 1/f .
A partir de la même relation i = C(dv/dt), vous pouvez voir que si dv/dt est constant et C est varié, une augmentation de C produit une augmentation de i, et une diminution de C produit une diminution de i.
Encore une fois, une augmentation de i signifie moins d'opposition (XC est moins), et une diminution de i signifie une plus grande opposition (XC est plus grand). Par conséquent, XC est inversement proportionnel à i et donc inversement proportionnel à la capacité.
XC est inversement proportionnel à fC, représenté par 1/fC .
La réactance capacitive, XC est en ohms lorsque f est en hertz et C est en farads. Notez que 2π apparaît au dénominateur comme une constante de proportionnalité. Ce terme est dérivé de la relation entre une onde sinusoïdale et le mouvement de rotation.


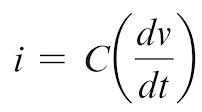
















Post a Comment