L'impédance
Dans la section précédente, nous avons obtenu les relations tension-courant
pour les trois éléments passifs comme:
Ces équations peuvent être écrites en termes de rapport de la tension du
phaseur au courant du phaseur comme:
A partir de ces trois expressions, on obtient la loi d’Ohm sous forme
complexe pour tout type d’élément comme:
où Z est une quantité dépendante de la fréquence appelée impédance,
mesurée en ohms.
L'impédance représente l'opposition que le circuit présente à la circulation
du courant sinusoïdal. Bien que l'impédance soit le rapport de deux
phaseurs, ce n'est pas un phaseur, car elle ne correspond pas à une grandeur
variant de manière sinusoïdale.
Les impédances des résistances, des inductances et des condensateurs peuvent
être facilement obtenues à partir de l'Eq. (9,39). Le tableau 9.3 résume
leurs impédances.
De la table, nous remarquons que ZL = jωL et ZC =
-j/ωC.
Prenons deux cas extrêmes de fréquence angulaire. Quand ω= 0 (c'est-à-dire
pour les sources CC). ZL = 0 et ZC → ∞ ,
confirmant ce que nous savons déjà - que l'inducteur agit comme un
court-circuit, tandis que le condensateur agit comme un circuit ouvert.
Quand ω → ∞ ,(c'est-à-dire pour les hautes fréquences). ZL = ∞ et
ZC = 0, indiquant que l'inductance est un circuit ouvert aux
hautes fréquences, tandis que le condensateur est un court-circuit. La
figure 9.15 illustre cela.
En tant que quantité complexe, l'impédance peut être exprimée sous forme
rectangulaire comme:
où R = ReZ est la résistance et X = ImZ est la
réactance. La réactance X peut être positive ou négative. On
dit que l'impédance est inductive lorsque X est positif ou capacitif
lorsque X est négatif. Ainsi, l'impédance Z = R + jX est dite
inductive ou retardée car le courant est en retard sur la tension, tandis
que l'impédance Z = R - jX est capacitive ou en avance parce que le
courant conduit la tension. L'impédance, la résistance et la réactance sont
toutes mesurées en ohms. L'impédance peut également être exprimée sous forme
polaire comme
Comparaison des équations. (9.41) et (9.42), nous en déduisons que :
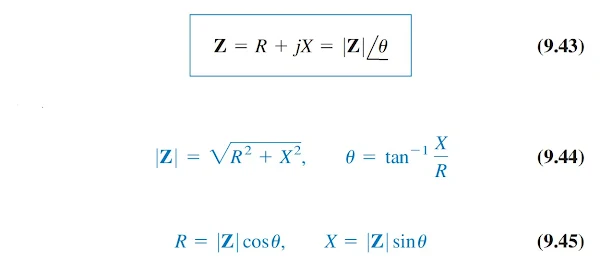
L'admittance
Il est parfois pratique de travailler avec la réciproque de l'impédance,
appelée admittance.
L'admittance Y est l'inverse de l'impédance, mesurée en siemens (S).
L'admittance d'un élément (ou d'un circuit) est le rapport du courant du
phaseur à travers celui-ci à la tension du phaseur à ses bornes, ou:
Les admittances des résistances, des inductances et des condensateurs peuvent être obtenues à partir de l'Eq. (9,39). Ils sont également résumés dans le tableau 9.3.
En tant que quantité complexe, nous pouvons écrire Y comme:
où G = ReY est appelée conductance et B = ImY est appelée susceptance. L'admittance, la conductance et la susceptance sont toutes exprimées en unité de siemens (ou mhos). De Eqs. (9,41) et (9,47),
Enregistrer un commentaire