amplificateur de différence
La tension de sortie d'un amplificateur différentiel est proportionnelle à la différence entre les deux tensions d'entrée. Pour le démontrer, nous analysons le circuit d'amplification différent représenté sur la figure 5.15, en supposant un ampli op idéal fonctionnant dans sa région linéaire. Nous dérivons la relation entre vo et les deux tensions d'entrée va et vb en additionnant les courants loin du nœud d'entrée inverseur:
Parce que l'ampli op est idéal, nous utilisons les contraintes de tension et de courant pour voir que:
Combiner Eq. 5.19, 5.20 et 5.21 donne la relation souhaitée:
L'équation 5.22 montre que la tension de sortie est proportionnelle à la différence entre une réplique à l'échelle de vb et une réplique à l'échelle de va. En général, le facteur d'échelle appliqué à vb n'est pas le même que celui appliqué à va.
Cependant, le facteur d'échelle appliqué à chaque tension d'entrée peut être rendu égal en définissant
Lorsque l'Eq. 5.23 est satisfaite, l'expression de la tension de sortie se réduit à:
L'équation 5,24 indique que la tension de sortie peut être une réplique à l'échelle de la différence entre les tensions d'entrée vb et va. Comme dans les circuits amplificateurs idéaux précédents, la mise à l'échelle est contrôlée par les résistances externes. En outre, la relation entre la tension de sortie et les tensions d'entrée n'est pas affectée par la connexion d'une résistance de charge non nulle aux bornes de la sortie de l'amplificateur.
Parce que l'ampli op est idéal, nous utilisons les contraintes de tension et de courant pour voir que:
Combiner Eq. 5.19, 5.20 et 5.21 donne la relation souhaitée:
L'équation 5.22 montre que la tension de sortie est proportionnelle à la différence entre une réplique à l'échelle de vb et une réplique à l'échelle de va. En général, le facteur d'échelle appliqué à vb n'est pas le même que celui appliqué à va.
Cependant, le facteur d'échelle appliqué à chaque tension d'entrée peut être rendu égal en définissant
Lorsque l'Eq. 5.23 est satisfaite, l'expression de la tension de sortie se réduit à:
L'équation 5,24 indique que la tension de sortie peut être une réplique à l'échelle de la différence entre les tensions d'entrée vb et va. Comme dans les circuits amplificateurs idéaux précédents, la mise à l'échelle est contrôlée par les résistances externes. En outre, la relation entre la tension de sortie et les tensions d'entrée n'est pas affectée par la connexion d'une résistance de charge non nulle aux bornes de la sortie de l'amplificateur.
Exemple
a) Concevez un amplificateur différentiel (voir Fig. 5.15) qui amplifie la différence entre deux tensions d'entrée par un gain de 8, en utilisant un ampli opérationnel idéal et des alimentations ± 8 V.
b) Supposons va = 1 V dans l'amplificateur différentiel conçu dans la partie (a). Quelle plage de tensions d'entrée pour ib permettra à l'ampli op de rester dans sa zone de fonctionnement linéaire?.
Solution
a) En utilisant l'équation simplifiée de l'amplificateur différentiel (Eq. 5.24),
Nous voulons deux résistances dont le rapport est 8. Regardez les valeurs de résistance réalistes énumérées dans l'annexe H. Choisissons Rb = 12 kΩ, donc Ra = 1,5 kΩ, bien qu'il existe de nombreuses autres possibilités. Notez que l'équation simplifiée de différence-amplificateur exige que:
Un choix simple pour Rc et Rd est Rc = Ra = 1,5 kΩ et Rd = Rb = 12 kΩ. Le circuit résultant est illustré à la Fig. 5.16.
b) Résolvez deux versions différentes de l'équation simplifiée de l'amplificateur de différence pour vo en termes de vb - en utilisant d'abord va = +8 V puis en utilisant va = -8V
Ainsi, si va = 1 V dans l'amplificateur différentiel de la partie (a), l'ampli op restera dans sa région de fonctionnement linéaire si:
FIN
Solution
a) En utilisant l'équation simplifiée de l'amplificateur différentiel (Eq. 5.24),
Nous voulons deux résistances dont le rapport est 8. Regardez les valeurs de résistance réalistes énumérées dans l'annexe H. Choisissons Rb = 12 kΩ, donc Ra = 1,5 kΩ, bien qu'il existe de nombreuses autres possibilités. Notez que l'équation simplifiée de différence-amplificateur exige que:
Un choix simple pour Rc et Rd est Rc = Ra = 1,5 kΩ et Rd = Rb = 12 kΩ. Le circuit résultant est illustré à la Fig. 5.16.
b) Résolvez deux versions différentes de l'équation simplifiée de l'amplificateur de différence pour vo en termes de vb - en utilisant d'abord va = +8 V puis en utilisant va = -8V
Ainsi, si va = 1 V dans l'amplificateur différentiel de la partie (a), l'ampli op restera dans sa région de fonctionnement linéaire si:
FIN





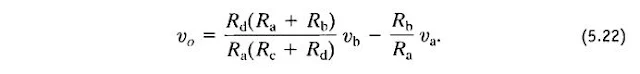






Post a Comment