Résistances en série
nous avons dit que lorsque seulement deux éléments se connectent à un seul nœud, ils sont censés être en série. Les éléments de circuit connectés en série transportent le même courant. Les résistances du circuit représenté sur la figure 3.1 sont connectées en série. Nous pouvons montrer que ces résistances transportent le même courant en appliquant la loi de courant de Kirchhoff à chaque nœud du circuit. L'interconnexion série de la figure 3.1 nécessite que:
figure 3.1
qui déclare que si nous connaissons l'un des sept courants, nous les connaissons tous. Ainsi, nous pouvons redessiner la figure 3.1 comme le montre la figure 3.2, en conservant l'identité du courant unique isPour trouver is, nous appliquons la loi de tension de Kirchhoff autour de la boucle fermée unique. Définir la tension aux bornes de chaque résistance comme une chute dans la direction de is donne:
L'importance de l'équ. 3.3 pour calculer is est que les sept résistances peuvent être remplacées par une seule résistance dont la valeur numérique est la somme des résistances individuelles, c'est-à-dire,
Ainsi, nous pouvons redessiner la figure 3.2 comme le montre la figure 3.3. En général, si k résistances sont connectées en série, la résistance unique équivalente a une résistance égale à la somme des k résistances, ou:
figure 3.3
Notez que la résistance de la résistance équivalente est toujours supérieure à celle de la plus grande résistance de la connexion série.
Une autre façon de penser à ce concept de résistance équivalente est de visualiser la chaîne de résistances comme étant à l'intérieur d'une boîte noire. (Un ingénieur électricien utilise le terme boîte noire pour désigner un récipient opaque; c'est-à-dire que le contenu est caché. L'ingénieur est ensuite mis au défi de modéliser le contenu de la boîte en étudiant la relation entre la tension et le courant à ses bornes. ) Il est impossible de déterminer si la boîte contient k résistances ou une seule résistance équivalente. La figure 3.4 illustre cette méthode d'étude du circuit représenté sur la figure 3.2.







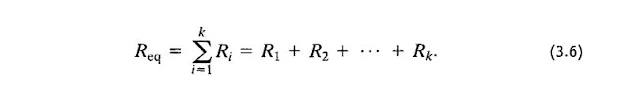


Post a Comment