introduction
L'étude des systèmes de numérotation est importante pour comprendre comment les données sont représentées avant de pouvoir être traitées par tout système numérique, y compris un ordinateur numérique. C'est l'un des sujets les plus fondamentaux de l'électronique numérique. Dans ce chapitre, nous aborderons différents systèmes de numération couramment utilisés pour représenter des données. Nous allons commencer la discussion avec le système de n ombres décimaux.
$ads={1}
Base décimale (10)
•La base décimale est la base de numérotation que nous utilisons de façon quotidienne pour calculer tous les grandeurs dans la vie comme la masse, poids, longueur, etc.
•Le système de nombre décimal est un système à nombre de radix-10 et comporte donc 10 chiffres différents ou symboles. Ce sont 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. Tous les nombres supérieurs après le «9» sont représentés en termes de ces 10 chiffres seulement.
•Rappelons que l'on écrit un nombre N en base 10 (système décimal), par exemple 135, sous la forme suivante : De façon générale si N est un entier positif contenant n chiffres alors :

Exemple:
3586.265
3586 = 3×10^3+ 5×10^2+ 8×10^1+ 6×10^0
0,265=2×10^-1 +6×10^-2 +5×10^-3
Base binaire (2)
•Le système de numération binaire est un système de numération à base 2 composé de "0" et de "1" en tant que deux chiffres indépendants. B=2 : {0 1 } •Tous les grands nombres binaires sont représentés sous la forme "0" et "1". La procédure d'écriture des nombres binaires d'ordre supérieur après «1» est similaire à celle expliquée dans le cas du système de nombres décimaux. exemple: 0, 1, 10, 11, 100, 101, 110,111, 1000, 1001, 1010, 1011
Base octale (8)
Le système de nombre octal a une base de 8 et a donc huit chiffres distincts. Tous les ordres supérieurs
•les nombres sont exprimés comme une combinaison de ceux-ci sur le même motif que celui suivi dans le cas des systèmes de nombres binaires et décimaux Les chiffres indépendants sont 0, 1, 2, 3, 4, 5, 6 et 7. Les 10 prochains chiffres qui suivent «7», par exemple, seront 10, 11, 12,
B=8 : {0 1 2 3 4 5 6 7 }
Exemple: 123,777,157,546,177,700
Base hexadécimale (16))
•Le système de nombres hexadécimaux est un système à 16 nombres à la base et ses 16 chiffres de base sont 0, 1, 2, 3,4, 5, 6, 7, 8, 9, A, B, C, D, E et F
B=16 : {0 1 2 3 4 5 6 7 8 9 A B C D E F}
Le système de nombres hexadécimaux fournit un moyen condensé de représenter de grands nombres binaires stockés et traités dans l'ordinateur.
Exemple: AB00,A05C,FFEE,…
logique combinatoire: conversion des bases
Conversion des nombres décimales vers nombres binaires
- Méthode de division
- Méthode de tableau de puissance de nombre 2 (méthode de soustraction successive)
- Méthode de forme générale de nombre entier
Conversion de binaire à décimale
Ou utilise le tableau comme ça: on additionne les colonne contient le nombre 1




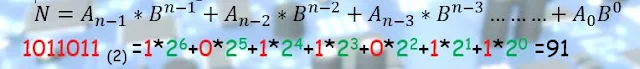



Post a Comment