les ports logiques
le port logique " NON " Inverseur (NOT Gate)
$ads={1}
Une porte NON ou Inverseur est un circuit logique à une entrée, une sortie dont la sortie est toujours le complément de la contribution. C'est-à-dire qu'une entrée "0" produit une sortie "1", et inversement. Quand interprété pour un positif système logique, un "0" logique à l’entrée produit un "1" logique à la sortie, et inversement. Il est également connu en tant que «circuit complémentaire» ou «circuit inverseur»
Symbole :
Table de vérité :
La ligne au-dessus de la lettre A est appelée "barre" et il exprime à inverse d'état logique , c'est à dire "1" inverse de "0" et "0"invers de "1" Alors nous écrivons : 1 = 0 , 0 = 1 .
Equation logique :
Schéma électrique :
Circuits intégrés :
la fonction OU (OR Gate )
Une porte OU effectue une opération addition logique sur deux ou plus de deux variables logiques. L'opération OU sur deux variables logiques indépendantes A et B est écrit Y = A + B et se lit Y égal Y OU B
Symbole, Equation logique :
Sur les schémas de circuits électroniques les fonctions logiques sont représentées par des symboles que l’on appelle généralement ”portes logiques”.
Table de vérité :
le port OU avec 3 et 4 entrées
Les figures ci-dessous représentent le symbole de circuit des portes OU à trois et quatre entrées et la table de vérité d'une porte OU à trois entrées. Les expressions logiques expliquant le fonctionnement des portes OU à trois entrées et à quatre entrées sont Y = A + B + C et Y = A + B + C + D

question :
Comment pourriez-vous implémenter matériellement une porte OU à quatre entrées en utilisant uniquement des portes OU à deux entrées?
la solution :
$ads={2}

La figure (a) montre un arrangement possible de portes OU à deux entrées simulant un OU à quatre entrées.
porte. A, B, C et D sont des entrées logiques et Y3 est la sortie. La figure (b) montre un autre arrangement possible. Dans le cas de la figure (a), la sortie de la porte OU 1 est Y1 = (A + B. La deuxième porte OU produit la sortie Y2 = Y1 + C = A + B + C.
De même, le la sortie de la porte OU 3 est Y3 = Y2 + D = A + B + C + D. Dans le cas de la figure (b), la sortie de la porte OU 1 est Y 1 = A + B. Le deuxième OU La porte produit la sortie Y2 = C + D. La sortie Y 3 de la troisième porte OU est donnée par Y1 + Y2 = A + B + C + D.
la fonction ET (AND Gate)
Une porte ET est un circuit logique ayant deux entrées ou plus et une sortie. La sortie d'une porte ET n'est HAUTE que lorsque toutes ses entrées sont à l'état HAUT ( état 1). Dans tous les autres cas, la sortie est BAS ( état 0).

question :
Montrer la disposition logique pour la mise en œuvre d'une porte ET à quatre entrées utilisant uniquement des portes ET à deux entrées
la solution :
La figure illustre l'implémentation matérielle d'une porte ET à quatre entrées utilisant des portes ET à deux entrées. La sortie de la porte ET1 est Y1 = AB La deuxième porte ET produit une sortie Y2 donnée par Y2 = Y1.C = ABC.
De même, la sortie de la porte ET3 est Y = Y2.D = ABCD et d'où le résultat

La fonction OU EXCLUSIF (XOR)
La fonction OU EXCLUSIF ne vaut 1 que si les deux entrées sont différentes. Elle s’écrit

La table de vérité et le symbole associés à cette fonction sont :
la question :
Comment implémenter des fonctions logiques EX-OR à trois et quatre entrées à l’aide de deux entrées Portes EX-OR?
la solution :
Les figures (a) et (b) illustrent la mise en œuvre d’une fonction logique EX-OR à trois entrées et d’une fonction logique à quatre entrées.
Fonction logique EX-OR utilisant des portes logiques à deux entrées:

Comment pouvez-vous implémenter un circuit NON en utilisant une porte EX-OR à deux entrées?
la solution :
Reportez-vous à la table de vérité d'une porte EX-OR à deux entrées reproduite à la figure (a). C'est clair de la vérité table que, si l’une des entrées de la porte est liée en permanence au niveau logique «1», l’autre entrée et sortie remplissent la fonction d'un circuit NOT. La figure (b) montre la mise en œuvre.

Réalisation d’une fonction logique XOR :
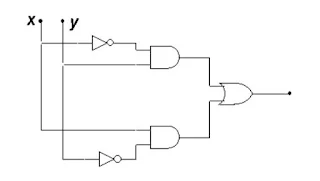
En combinant entre elles les différentes portes logiques on peut à priori réaliser n’importe quelle fonction logique. On appelle logigramme la réalisation d’une fonction complexe à l’aide des portes de base. A titre d’exemple réalisons la fonction OU EXCLUSIF (XOR) en n’utilisant que des portes NON, ET, OU.

La fonction NON ET (NAND)
La fonction NON ET est obtenue en complémentant la fonction ET
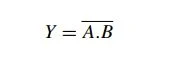

La fonction NON OU (NOR).
La fonction NON OU est obtenue en complémentant la fonction OU :


En général, l’expression booléenne d’une porte NOR comportant plus de deux entrées peut être écrite en tant que














Post a Comment