Code BCD : Binary Coded Decimal
La décimale codée binaire (BCD) est un type de code binaire utilisé pour représenter un nombre décimal donné sous une forme binaire équivalente. Les conversions de BCD à décimales et décimales à BCD sont très simples et rapides.
Code BCD :
Le code Gray a été conçu par Frank Gray chez Bell Labs et breveté en 1953. Il s’agit d’un code binaire non pondéré dans lequel deux valeurs successives ne diffèrent que d’un bit. Grâce à cette fonctionnalité, l’erreur maximale pouvant s’insinuer dans un système utilisant le code Gray binaire pour coder les données est bien inférieure à l’erreur la plus défavorable rencontrée dans le cas du codage binaire direct.
Applications
1.Le code Gray est utilisé dans la transmission de signaux numériques car il minimise l’occurrence des erreurs.
2. Le code Gray est préférable au code binaire droit dans les appareils de mesure d'angle.
Utilisation de code Gray élimine presque la possibilité d'une erreur de lecture d'un angle, ce qui est probable si l'angle est représenté sous forme binaire droite. La propriété cyclique du code Gray est un atout dans cette application.
3. Le code Gray est utilisé pour marquer les axes des cartes de Karnaugh, une technique graphique utilisée pour minimisation des expressions booléennes.
4. L'utilisation de codes Gray pour adresser la mémoire de programme dans les ordinateurs minimise la consommation d'énergie.
Cela est dû au fait que moins de lignes d’adresses changent d’état avec des avancées dans le compteur de programme.
5. Les codes gris sont également très utiles dans les algorithmes génétiques car les mutations dans le code permettent principalement changements progressifs. Cependant, un changement d’un bit peut parfois occasionner un grand saut, conduisant ainsi à de nouvelles propriétés.
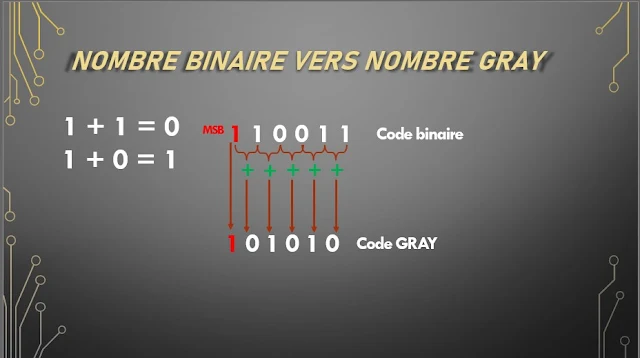
Conversion nombre Binaire vers nombre Gray
1. Commencez par le bit le plus significatif (MSB) du nombre binaire. Le MSB de l'équivalent de code Gray est le même que le MSB du nombre binaire donné.
2. Le deuxième bit le plus significatif, adjacent au MSB, dans le numéro de code Gray est obtenu en ajoutant le MSB et le second MSB du nombre binaire et en ignorant le report éventuel. C’est-à-dire que si le bit de poids fort et le bit qui lui est adjacent sont tous deux "1", le bit de code Gray correspondant serait un "0".
3. Le troisième bit le plus significatif, adjacent au deuxième MSB, du numéro de code Gray est obtenu en ajoutant le deuxième MSB et le troisième MSB au nombre binaire et en ignorant le report éventuel.
4. Le processus se poursuit jusqu'à l'obtention du LSB du numéro de code Gray par l'addition du LSB et du bit adjacent supérieur le plus proche du nombre binaire.
Conversion nombre Gray vers nombre Binaire
1. Commencez par le bit le plus significatif (MSB). Le MSB du nombre binaire est identique au MSB du numéro de code Gray.
2. Le bit situé à côté du MSB (le second MSB) du nombre binaire est obtenu en ajoutant le MSB du nombre binaire au second MSB du numéro de code Gray et en ignorant le report éventuel.
3. Le troisième MSB du nombre binaire est obtenu en ajoutant le deuxième MSB du nombre binaire au troisième MSB du numéro de code Gray. Encore une fois, carry, le cas échéant, doit être ignoré.
4. Le processus continue jusqu'à l'obtention du LSB du nombre binaire.




Post a Comment